I am currently writing another version that uses %d4-%d7 for the accumulated result. It'll be tricky since %d0-%d3 are the operands themselves, and I need another register or two for temporary calculations. I'm planning on first calculating all partial products that need %d3 so that can be freed first. I still might have to unload a register into an address register so I have enough data registers available for the second half of partial products. Also, I won't be able to do as many staggered long additions, but the speed gains by using registers vs the stack should make up for that.
Anyway, here's the code, which includes the C interface mul64:
Code: .if 0
HAHAHA! Sweet optimization note: any two longs (as a result of multiplying two words) can be added without carry if they are staggered. The largest product of two 16-bit unsigned values is 0xFFFE0001, so staggering the adds like so will never carry:
FFFE00010000
0000FFFE0001
------------
FFFEFFFF0001
These can be chained like so without carry.
.endif
| this routine currently uses the following partial product layout:
|exploiting the no-carry trick noted above:
|first partial product:
|0055ddff +
|.44ccee.
|second partial product:
|.1166bb. +
|..88aa..
|third partial product:
|..2277.. +
|...99...
|fourth partial product:
|...33...
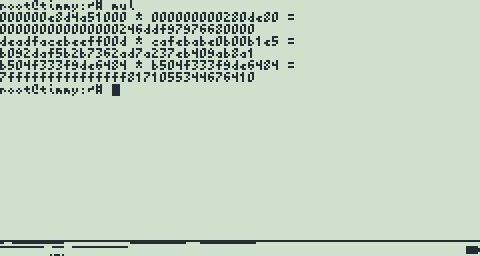
| multiply unsigned 64-bit integers
| return unsigned 128-bit integer
| input:
| x = %d0:%d1
| y = %d2:%d3
| output:
| x*y = %d0:%d1:%d2:%d3
| 2326 cycles (74 cycles per mulu)
mulu64:
| save registers
movem.l %d4/%a0-%a1,-(%sp)
|// first partial product
|// 0055ddff
|push:
|ff << 0 dh
|dd << 2 df
|55 << 4 bf
|00 << 6 ae
| ab:cd d0:d1
| ef:gh d2:d3
| dh
move.w %d1,%d4
mulu.w %d3,%d4 | dh
move.l %d4,-(%sp)
| df
move.w %d1,%d4
mulu.w %d2,%d4 | df
move.l %d4,-(%sp)
| bf
move.w %d0,%d4
mulu.w %d2,%d4 | bf
move.l %d4,-(%sp)
| ae
swap %d2
| ab:cd d0:d1
| fe:gh d2:d3
move.l %d0,%d4
swap %d4
mulu.w %d2,%d4 | ae
move.l %d4,-(%sp)
|
|// .44ccee.
|add without carry:
|ee << 1 dg
|cc << 3 de
|44 << 5 be
| dg
move.w %d1,%d4
swap %d3
| ab:cd d0:d1
| fe:hg d2:d3
mulu.w %d3,%d4 | dg
add.l %d4,5*2(%sp)
| de
move.w %d1,%d4
mulu.w %d2,%d4 | de
add.l %d4,3*2(%sp)
| be
move.w %d0,%d4
mulu.w %d2,%d4 | be
add.l %d4,1*2(%sp)
|
|// second partial product
|// .1166bb.
|push:
| 0x0 << 0 // don't really need this
|bb << 1 ch
|66 << 3 bg
|11 << 5 af
| 0x0 << 7
| ch
swap %d1
| ab:dc d0:d1
| fe:hg d2:d3
move.l %d3,%d4
swap %d4
mulu.w %d1,%d4 | ch
move.l %d4,-(%sp)
| bg
move.w %d0,%d4
mulu.w %d3,%d4 | bg
move.l %d4,-(%sp)
| af
swap %d0
| ba:dc d0:d1
| fe:hg d2:d3
move.l %d2,%d4
swap %d4
mulu.w %d0,%d4 | af
move.l %d4,-(%sp)
clr.w -(%sp)
|
|// ..88aa..
|add without carry:
|aa << 2 cg
|88 << 4 ce
| cg
move %d1,%d4
mulu.w %d3,%d4 | cg
add.l %d4,4*2(%sp)
| ce
move %d1,%d4
mulu.w %d2,%d4 | ce
add.l %d4,2*2(%sp)
|
|add with carry (upper 7 words or 3.5 longs)
lea 7*2(%sp),%a1 | second partial product
lea 7*2+7*2(%sp),%a0 | result
addx.l -(%a1),-(%a0)
addx.l -(%a1),-(%a0)
addx.l -(%a1),-(%a0)
addx.w -(%a1),-(%a0)
| pop off our second partial product
lea 7*2(%sp),%sp
|
|// third partial product
|// ..2277..
|push:
|0x00 << 0 // don't really need this
|77 << 2 bh
|22 << 4 ag
|0x00 << 6
| bh
move.l %d0,%d4
swap %d4
swap %d3
| ba:dc d0:d1
| fe:gh d2:d3
mulu.w %d3,%d4 | bh
move.l %d4,-(%sp)
| ag
swap %d3
| ba:dc d0:d1
| fe:hg d2:d3
move.w %d0,%d4
mulu.w %d3,%d4 | ag
move.l %d4,-(%sp)
clr.l -(%sp)
|
|// ...99...
|add without carry:
|99 << 3 cf
| cf
move.w %d1,%d4
swap %d2
| ba:dc d0:d1
| ef:hg d2:d3
mulu.w %d2,%d4 | cf
add.l %d4,3*2(%sp)
|
|add with carry (upper 6 words or 3 longs)
lea 6*2(%sp),%a1 | third partial product
lea 6*2+6*2(%sp),%a0 | result
addx.l -(%a1),-(%a0)
addx.l -(%a1),-(%a0)
addx.l -(%a1),-(%a0)
| pop off the third partial product
lea 6*2(%sp),%sp
|
|// fourth partial product
|// ...33...
|push:
|0x00 << 0 // don't really need this
|0x0 << 2 // or this
|33 << 3 ah
|0x0 << 5
|0x00 << 6
| ah
move %d0,%d4
swap %d3
| ba:dc d0:d1
| ef:gh d2:d3
mulu.w %d3,%d4 | ah
move.l %d4,-(%sp)
clr.w -(%sp)
clr.l -(%sp)
|
|add with carry (upper 5 words or 2.5 longs)
lea 5*2(%sp),%a1 | fourth partial product
lea 5*2+5*2(%sp),%a0 | result
addx.l -(%a1),-(%a0)
addx.l -(%a1),-(%a0)
addx.w -(%a1),-(%a0)
| pop off fourth partial product
lea 5*2(%sp),%sp
| pop off result and saved registers
movem.l (%sp)+,%d0-%d4/%a0-%a1
rts
.global mul64
| void mul64(int64 *a, int64 *b, int128 *result);
mul64:
| save
move.l %d3,-(%sp)
move.l 4+4(%sp),%a0
move.l 4+4+4(%sp),%a1
movem.l (%a0)+,%d0-%d1
movem.l (%a1)+,%d2-%d3
jbsr mulu64
move.l 4+4+4+4(%sp),%a0
lea 4*4(%a0),%a0
movem.l %d0-%d3,-(%a0)
| restore
move.l (%sp)+,%d3
rts