| Author |
Message |
|
Weregoose
Authentic INTJ
Super Elite (Last Title)
Joined: 25 Nov 2004
Posts: 3976
|
 Posted: 27 Sep 2005 03:47:58 am Post subject: |
|
|
Constant and Integer Approximations
As a celebratory gesture for my reaching 500 posts, I'd like to ignite some interest in a small piece of mathematics that has fascinated me for some time. Starting off, I'd like to reintroduce the concept of continued fractions, which has been noted [post="46558"]once[/post] or twice by Sir Robin.
What are continued fractions?
Continued fractions are a series of nested integers in their inverse forms that, when ordered properly, yield an approximation (or equivalent) of some selected value.
The way I see continued fractions, they act as sort of a behind-the-curtain crew for mathematics. By opening up these curtains and revealing the inner workings of otherwise nonsensical configurations, we are able to learn the secret design of certain numbers, how they are built, and whatever relationships they hold towards each other and to mathematics as a whole.
How are continued fractions used?
Alright. Let's say we have the number 16.184. That's almost 16, but not quite—we need a little more.
We can add 1/5 to get it closer. The resulting 16.2 is okay, but it's still not exact.
Tossing in another fraction gives us 16+1/(5+1/2), which is 16.1818…, or 178/11.
We can continue adding fractions in this manner until we come up with a fitting equivalent.
In this case, 16.184 is calculated precisely with 16+1/(5+1/(2+1/(3+1/3)))—we have our continued fraction.
How does one know exactly what to add each time?
Now, wait a minute! Where the heck did I get all those fractions?
Well, let's take 16.184 again. If we remove the integer part and put it aside, then we're left with a decimal.
If we invert this decimal, then we should get another number with an integer part.
Take that integer, too, and put it next to the first number we encountered.
Repeat this process until you have nothing left to find the inverse of, and you get the following series of numbers:
16 5 2 3 3
If we place the expression [font="courier new;font-size:9pt;line-height:100%;color:darkblue"]+1/( between each one of these numbers, then we're suddenly left with a familiar continued fraction that is again equal to 16.184.
The formal way to write this is: {16;5,2,3,3}
The first number is separated by a semicolon to indicate that it is the integer part of the original number.
Here is another example: 1.234
We can remove the integer and find the inverse of what remains in one quick gesture: [font="courier new;font-size:9pt;line-height:100%;color:darkblue"]1/fPart(Ans
Just make sure that you have the right number stored to [font="courier new;font-size:9pt;line-height:100%;color:darkblue"]Ans in the first place.
Pressing [ENTER] repeatedly while recording each integer as it comes up will give us our desired list of numbers.
The end result should be: {1;4,3,1,1,1,10}
This is shorthand for 1+1/(4+1/(3+1/(1+1/(1+1/(1+1/10)))))
Now, what'll happen if we attempt to write out a continued fraction for an irrational number (i.e., a number which cannot be written as a fraction)?
We can take the square root of three for this purpose: 1.7320508075689…
The inverse of its decimal is roughly 1.3660254037844.
Subtracting the one and calculating the inverse of .3660254037844 gives us 2.7320508075689—hold it!
Isn't that 1+√3? It is, exactly. Continuing on, and we get... 1.3660254037844, again!
Repeating the process alternates between the two numbers indefinitely.
So, does something strange happen to the square root of two?
Yes—Right off the bat, something goes screwy.
The first inverse we calculate is already equal to the square root of two by itself plus one, and then that number repeats itself forever.
So, √2 = 2+1/(2+1/(2+1/…
Now we'll try something a little bit different: How about the natural logarithmic base (e)?
This one is not as apparent at first, but after writing down more numbers, the pattern should become more obvious.
Note: This is where I should bring up something important concerning the calculator's ability to handle decimals with precision. Bottom line, it doesn't do its job very well. Two examples which make this obvious are [font="courier new;font-size:9pt;line-height:100%;color:darkblue"]fPart(√(3)²) and [font="courier new;font-size:9pt;line-height:100%;color:darkblue"]i^7. That said, the patterns of certain continued fractional representations of various constants begin to break down due to floating point errors, the technicalities of which can be left without explanation for now.
...and from that we get {2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,…}
What can we learn from continued fractions?
Remember when I "tossed in another fraction" and then compared 178/11 to 16.184? One of the more useful concepts that comes with the nature of continued fractions is the wonderful ability to approximate adherently cryptic values. Take [font="times new roman"]π, for instance. We all know that it's hard to approximate using a less methodical approach; brute force can eventually coincide two values (the divisor of which being roughly [font="times new roman"]π), but that can take a while.
If you've ever attempted this, then you either found 22/7 pretty quickly, or you went sailing headlong into the direction of 3141592653/1000000000. I doubt that several people have had the determination to discover 333/106, or 355/113, which is arguably the most useful fractional approximation for [font="times new roman"]π.
So, what makes a number either easier or harder to approximate? It's an odd question, but in truth there are tell-tale signs as to whether a number will yield a fractional substitute quickly. When looking for integers in continued fractions, the larger they come (and how early on) determines the accuracy at which the target value is approximated.
[font="times new roman"]π^4 (97.409091034003…) is a brilliant example. When you begin to draw the curtains open on this one, you should start seeing some interesting numbers...
2.4444436980564 Easy approximation!
2.2500037785958 …
3.9999395433810 …
1.0000604602742 The smaller the decimal, the larger the inverse, yes?
16539.786053435 Bingo.
In the fifth step, we get a much larger number. This usually entails that a fine approximation with fractions is available. To find it, we must insert our list of integers into the expanded form, which will consist entirely of nice, rational numbers. Also, the specific fraction that we are looking for is parked directly behind the larger value we came across.
{97,2,2,3,1,16539,1,…}
Tip: If you intend to keep a specific range of numbers, and there is a one directly trailing it, then take that along, too!
Reason: A+1/(B+1/(C+1/1)) = A+1/(B+1/(C+1))
Thus, we can bring our list down to: {97,2,2,3,1,16540}
Now, we begin with 97 (97/1); add another fraction to get 97.5 (195/2), and carry on for the following: 487/5, 1656/17, 2143/22*screech* ...and the calculator stops us there.
Fair enough—we got some very nice approximations. So nice, in fact, that if we multiply the denominator in the last result by the original number, then we get something extraordinary:
22[font="times new roman"]π^4 ≈ 2143.0000027481
Inexplicable, perhaps, to those untrained in number theory—but these mathematics spell it out quite nicely.
When used purposefully, continued fractions can teach us many things like this, and at a very good pace.
The next thing I'd like to show you is how to use constants in complex equations to keenly approximate certain values, while following a set of rules.
Keen Approximations [Article]
Keenness, as defined by Ed Pegg Jr., equals log10(max(CF))/complexity, where max(CF) is the number of correct digits in the approximation and complexity is the number of digits used within the approximation. Here are his exact rules:
- Each digit or constant used adds 1 to the complexity. Each function adds 1 to the complexity.
- Division, multiplication, addition, subtraction, exponentiation, parenthesization are free. In 1/x, or in x^-1, the 1 is free.
- Asymptotic functions, such as Zeta or cos(1+cos(1+cos(x))), are not allowed, nor are Pisot numbers.
- Root objects, such as Pi ~ {1+x+6x^2+x^3-5x^4-5x^5+2x^6}2 can be thought of as {1,1,6,1,-5,-5,2}2 (complexity 8). Zeros count.
This takes some practice. Sometimes it is difficult to determine exactly what counts in complexity, but you can use this central Keenness Table along with the constants (listed down below) to experiment your way inside learning what is meant by the equation.
Famous Constants
In forming an approximation that is more elaborate than a simple fraction, a broad view of mathematics plus a wide usage of different kinds of functions will only take you so far—you need to include the right set of numbers, too.
To make this easier, here are the constants with their numerical values, calculated only to the number of decimals that the calculator is capable of retaining to a single letter variable. In other words, rest assured, adding another digit to the end of any of these numbers will not affect their outcomes from within any equation on the calculator.
[font="courier new"]1.6180339887499→Φ or 2cos(36°→Φ or e^(sinh‾¹(.5→Φ
0.5772156649015→γ
‾2.502907875095→α
2.6854520010650→K
0.9159655941772→G
The constants listed above, from top to bottom, are called: Golden Ratio, Euler-Mascheroni Constant, Feigenbaum alpha, Khinchin constant, and Catalan constant. Because each constant is different, they provide the range and flexibility necessary for building a stronger foundation for approximation. However, as each constant that is used is worth one point towards total complexity, they need to be used wisely.
Known Approximations
All of the approximations contained in the Keenness Table are known. I'll provide links to different lists of approximations here. The Golden Ratio does not have a page to itself, but with some creativity, one should be able to manipulate equations meant for other constants yet contain Phi so that Phi itself is approximated.
Pi Approximations
Euler-Mascheroni Constant Approximations
Feigenbaum Constant Approximations (Does not include Feigenbaum alpha)
Khinchin's Constant Approximations
Catalan's Constant Approximations
Weregoose's Approximations
In honor of my new customizable status (I was Supergoose at the time of writing this), this section will be named after the handle that I normally use across the Internet.
These will all be written in the format shown on the calculator, with roots transformed into fractional exponents.
The approximations listed here aren't necessarily keen, but they certainly were fun to try out. After naming Phi to P, Euler's constant to Y, Feigenbaum's alpha to A, and then the Khinchin and Catalan constants to their respective letter representations, play around with some of these and then see what you can do to make your own. Consider this the finale... Have fun!
[font="courier new"]▫ 40937γ^.5/9900 ≈ [font="times new roman"]π
▫ 165(γ-2/(G+K))-.61 ≈ 3
▫ 405γ/e ≈ 86
▫ 2^(γ^‾3.6)-.2 ≈ 150
▫ 90(6Φ-α) ≈ 1099
▫ 4e^4/(95log(Φ)) ≈ 11
▫ 1-[font="times new roman"]π+ln(129+8/999) ≈ e
▫ 2ln(3+3333/3733) ≈ e
▫ (941^2+1)^(1/([font="times new roman"]π19^.5)) ≈ e
▫ (e^3(11^4+59/9))^(1/11) ≈ [font="times new roman"]π
▫ 2(1.6635/[font="times new roman"]π)^(1/3) ≈ Φ
▫ γ^‾6-.1(7^‾.5) ≈ 27
▫ 297(e+G/6)-.67 ≈ 852
▫ 88ln(89) ≈ 395
▫ αγΦG+[font="times new roman"]π-1/2329 ≈ 1
▫ (52+1/126)^(1/4) ≈ K
▫ (2824/7)^(1/6)+1/4010007 ≈ e
▫ 375γ^.4 ≈ 301
/Goose
Last edited by Guest on 14 Nov 2006 11:26:34 pm; edited 1 time in total |
|
| Back to top |
|
|
threefingeredguy
Advanced Member
Joined: 01 Sep 2005
Posts: 479
|
| Posted: 27 Sep 2005 09:06:32 am Post subject: |
|
|
| Thats cool! I understand it, but just barely. Are there any real world applications of this? |
|
| Back to top |
|
|
Brazucs
I have no idea what my avatar is.
Super Elite (Last Title)
Joined: 31 Mar 2004
Posts: 3349
|
| Posted: 27 Sep 2005 03:40:08 pm Post subject: |
|
|
You should get the Mircea-Mugure approximation of the golden ratio up. That's the only one I know  |
|
| Back to top |
|
|
alexrudd
pm me if you read this
Bandwidth Hog
Joined: 06 Oct 2004
Posts: 2335
|
| Posted: 27 Sep 2005 06:44:53 pm Post subject: |
|
|
I made it through about half of it before getting a headache. I understand the repeating fractions part, and some of the method used for finding the approximations, but read through it too quickly after that. If I ever feel the urge, I'll go read it again. :)
How long did it take you to find each approximation?
Thank God the BASIC contest doesn't have anything to do with pure math. |
|
| Back to top |
|
|
Arcane Wizard
`semi-hippie`
Super Elite (Last Title)
Joined: 02 Jun 2003
Posts: 8993
|
| Posted: 27 Sep 2005 06:56:51 pm Post subject: |
|
|
Supergoose wrote: Now, wait a minute! Where the heck did I get all those fractions?[post="57163"]<{POST_SNAPBACK}>[/post] That's exactly what I've wondered since I learned about continued fractions! Thanks a lot for the explanation, I liked it. : )
Though I don't have any math classes any more so I can't show off about this.  
Last edited by Guest on 27 Sep 2005 06:57:54 pm; edited 1 time in total |
|
| Back to top |
|
|
Weregoose
Authentic INTJ
Super Elite (Last Title)
Joined: 25 Nov 2004
Posts: 3976
|
| Posted: 27 Sep 2005 10:44:47 pm Post subject: |
|
|
Quote: Are there any real world applications of this? I'm unsure of how much of a direct impact it has had in the field of mathematics, but stumbling innocently into an peculiarly good approximation will suggest that something exists between the lines of what is being looked at—This typically coerces mathematicians to look deeper into the situation just to pinpoint exactly what is going on. Previously overlooked connections in mathematics can be discovered accordingly.
I mean, take a look at the fourth root of nine point one.
9.1^(1/4) ≈ 1.7368421418769
This produces a stunning continued fraction series:
1.3571427897063
2.8000005287027
1.2499991739026
4.0000132176021
75656.688137102
This leads us to the approximation of 33/19, which is very simple. That can be attributed to the following:
9.1^(1/4)^4 ≈ (33/19)^4
9.1 ≈ 33^4/19^4
91/10 ≈ 1185921/130321
(10 × 91)/(91 × 10) ≈ (10 × 1185921)/(91 × 130321)
1 ≈ 11859210/11859211
Interestingly enough, 11859210 and 11859211 are the "two highest consecutive numbers…that both have all prime factors equal or less than 19."
Quote: You should get the Mircea-Mugure approximation of the golden ratio up. Could you show this to me? I can't find anything about it! 8)
It does bring up something I want to show you, though.
Kudos to whoever can complete the continued fraction series for Ф! :D
Also related to Phi...
Take the most recent number you used in your calculator (RAM, program, wherever you can get one).
If none is available, take the first number you can find around you.
When you have it, type it up on the home screen and press [ENTER].
Type [font="courier new"]Ans‾¹+1 and press [ENTER].
Keep pressing that key until the convergence is complete... :lol:
When that's done, pick a new number and do the same with [font="courier new"]1/(Ans+1.
Here, you should get the inverse of Ф, which is also Ф-1 and Ф²-2.
Quote: How long did it take you to find each approximation? I have an hour or two each day at college, and a bus ride back into my town. Plenty of time for my inner nerd to party.
Quote: Thanks a lot for the explanation, I liked it. My aim was to give the explanation I was never able to receive. 
Last edited by Guest on 27 Sep 2005 10:46:32 pm; edited 1 time in total |
|
| Back to top |
|
|
thornahawk
μολών λαβέ
Active Member
Joined: 27 Mar 2005
Posts: 569
|
| Posted: 29 Sep 2005 07:33:25 am Post subject: |
|
|
I want to add my small bits:
Everyone apparently knows now that numbers can be represented as continued fractions. What is probably less known is that functions, yes functions, can also be represented as continued fractions.
Here are some of my favorite examples:
Natural logarithm:
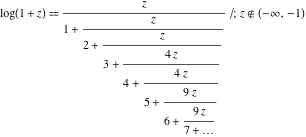
Inverse tangent:
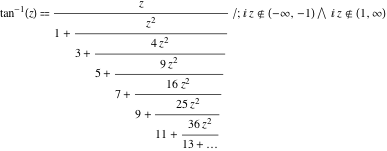
(from functions.wolfram.com)
The patterns for the general terms are pretty nice for these functions. A practical use for these is that some programs use these continued fractions for computing approximations to them.
I come now to my second bit: how do you PROPERLY evaluate a continued fraction? The most obvious way is to start from the right (or as continued fraction specialists call it, the "tail") and work eventually to the left. Two fundamental problems arise: one, you have to guess how far you should start, and two, there is no way take advantage of the labors you had if you had to recompute the continued fraction with more terms. So what is the right way?
Only relatively recently has an algorithm been proposed: it's called Lentz's algorithm.
Say you have the continued fraction
b(0) + a(1)/(b(1) + a(2)/...)
The algorithm in TI-BASIC would look something like this:
Code:
b(0)→Y
(Y=0)e-45+Y→Y
Y→C:0→D
1→J
Repeat abs(H-1)<e-12
b(J)+D*a(J)→D
((D=0)e-45+D)ֿ¹→D
b(J)+a(J)/C→C
(C=0)e-45+C→C
CD→H:HY→Y
\\do whatever updates you need to do for a() and b(), e.g. J+1→J
End
with the converged continued fraction stored in Y. (Optimization freaks, do your worst. ) The 10^-45 in there is needed to prevent division by zero errors.  I have forgotten the original reference for this nifty algorithm, though. :(
Last bit I want to add, you might want to Google around for "periodic continued fractions". The golden ratio and √2 are excellent samples.
That's all, folks. ;)
thornahawk (~_~)
P.S. Haven't posted in a while, so I thought I'd add content.
Last edited by Guest on 29 Sep 2005 07:35:27 am; edited 1 time in total |
|
| Back to top |
|
|
Weregoose
Authentic INTJ
Super Elite (Last Title)
Joined: 25 Nov 2004
Posts: 3976
|
| Posted: 29 Sep 2005 12:47:12 pm Post subject: |
|
|
Yes, the algorithm I've been using is this:
[font="courier new"]L1(dim(L1
For(I,dim(L1)-1,1,‾1
Ans‾¹+L1(I
End
Disp Ans►Frac
Lentz's algorithm looks more promising (I saw the pseudo code for it, and that was frightening), but I'm wondering something: Is not every term [font="courier new"]aJ equal to one? With that, I'd finally be able to try this out.
Thank you for your contributions. :)
[EDIT]
Optimized, and changed for readability:
[font="courier new"]b0
Ans+E‾45not(Ans→Y
DelVar DAns→C
1→J
Repeat E‾12>abs(H-1
bJ+DaJ
1/(Ans+E‾45not(Ans→D
bJ+aJ/C
Ans+E‾45not(Ans→C
AnsD→H:AnsY→Y
Updating variables—I already have this worked out for lists, but I need an answer first
End
Last edited by Guest on 19 Jun 2007 06:50:57 pm; edited 1 time in total |
|
| Back to top |
|
|
thornahawk
μολών λαβέ
Active Member
Joined: 27 Mar 2005
Posts: 569
|
| Posted: 29 Sep 2005 01:16:43 pm Post subject: |
|
|
Simple continued fractions are the continued fractions where all the a's (in my notation, that is... ) are equal to one. CF's (sorry, "continued fraction" seems a wee bit long for me ) in general can have any complex number as their a's and b's. Of course, not all CF's converge given that kind of freedom (e.g, substitute any negative z in the CF for the natural logarithm I just gave).
For the case of CF-expanding a real number, the a's and b's, for simplicity, are taken as integers. Further simplification can be done by manipulating the CF such that all the a's are unity (hence "simple" ).
In your case, Goose, since you're investigating CF-expansions of reals, you can change all the a's to 1 in the code, and I suppose since you're storing the b's in a list, b(j) would correspond to L1(j+1). ;)
BTW, in the code, 10^-12 is the appropriate tolerance for TI calculators I arrived at through experimentation. If you're interested in seeing the individual convergents, you might want to insert a Disp Y►Frac and/or append Y to some other list at the beginning of the Repeat loop.
thornahawk
P.S. I guess I could include a listing of the code I use on my TI-83 to compute the Euler-Mascheroni constant, if anyone's interested. ;)
P.P.S Michael Trott must have been really bored:
http://mathworld.wolfram.com/TrottsConstant.html
(stylistic edit(s) done)
Last edited by Guest on 19 Jun 2007 06:50:12 pm; edited 1 time in total |
|
| Back to top |
|
|
DarkerLine
ceci n'est pas une |
Super Elite (Last Title)
Joined: 04 Nov 2003
Posts: 8328
|
| Posted: 29 Sep 2005 07:25:39 pm Post subject: |
|
|
SCF's only: (I hope I optimized this right, see no objections but then I might not)
Code:
e-45 -> E
L1(1
Ans+Enot(Ans->Y
DelVar DAns->C
For(J,1,e3
D+L1(J
1/(Ans+Enot(Ans->D
L1(J)+1/(C+Enot(C->C
J+e3(1≠round(CD,12->J
YCD->Y
End
About Trott's constant... how does anyone know that further digits exist? what if at some point no digit you added would work? wouldn't that invalidate the whole concept?
Last edited by Guest on 29 Sep 2005 09:11:57 pm; edited 1 time in total |
|
| Back to top |
|
|
thornahawk
μολών λαβέ
Active Member
Joined: 27 Mar 2005
Posts: 569
|
| Posted: 29 Sep 2005 09:07:38 pm Post subject: |
|
|
I have forgotten to add that if it can be shown that C and D won't be zero in your particular case (which, IIRC, is often the case with SCF's), the lines with the 10^-45 "kludge" can be safely removed, thus:
Code:
L1(1→Y
DelVar DAns→C
For(J,1,e3
1/(D+L1(J→D
Cֿ¹+L1(J→C
J+e3(1≠round(CD,12→J
YCD→Y
End
...as I understand from your SCF-optimized implementation, Sir Robin. :)
You can of course go back to the original implementation if "divide by zero" errors start rearing their butt-ugly heads. ;)
"...how does anyone know that further digits exist? what if at some point no digit you added would work? wouldn't that invalidate the whole concept?"
IIRC, it's not even known if Trott's constant is irrational, much less transcendental (which implies an infinite SCF expansion, since rational numbers have terminating SCF's by virtue of their definition).
OT, I've talked to the guy, and he's really weird. Seems as if he's really keen at mathematical finagling. His "art" is awesome, though: http://www.graphica.com/gallery/
thornahawk
P.S. I still find it abhorrent to monkey around with For( loop indices. |
|
| Back to top |
|
|
DarkerLine
ceci n'est pas une |
Super Elite (Last Title)
Joined: 04 Nov 2003
Posts: 8328
|
| Posted: 29 Sep 2005 09:12:21 pm Post subject: |
|
|
I wouldn't need to monkey if TI-83+ Basic had a Break command.
Edit: wouldn't that algorithm fail rather beautifully if the b0 were 0? Y would then continue being 0 for quite a long time... This also might be a simple case disproving that C and D can never be 0.
Also, the boundary for J needs to be dim(L1 rather than e3. I mean, what if you run out of indices?
Last edited by Guest on 29 Sep 2005 09:16:20 pm; edited 1 time in total |
|
| Back to top |
|
|
thornahawk
μολών λαβέ
Active Member
Joined: 27 Mar 2005
Posts: 569
|
| Posted: 29 Sep 2005 09:27:22 pm Post subject: |
|
|
"I wouldn't need to monkey if TI-83+ Basic had a Break command."
That reminds me of the "Things I wish TI calculators had" thread I posted a while back. ;)
"... the boundary for J needs to be dim(L1 rather than e3. I mean, what if you run out of indices?"
That was a direct mod of your code, but you're right, the loop boundary has to be the list dimension.
"...wouldn't that algorithm fail rather beautifully if the b0 were 0?"
In that case, you cheat by starting at b1, running the loop and appending the line a1/Y. :P
thornahawk |
|
| Back to top |
|
|
Weregoose
Authentic INTJ
Super Elite (Last Title)
Joined: 25 Nov 2004
Posts: 3976
|
| Posted: 03 May 2006 12:08:27 pm Post subject: |
|
|
A page has been added for Golden Ratio Approximations.
Is anyone willing to help me in this most excellent quest? |
|
| Back to top |
|
|
|
Math and Science => Technology & Calculator Open Topic
